III. Two Regimes of Common Time

Connecting the independent Carrollian times at each point in space with large scale common time of everyday experience and the small scale common time of quantum mechanics.

While there are lots of takes out there in physics that space, time, or spacetime are emergent — generally from quantum mechanics (QM) — let me motivate the possibility that it’s just the sense of “common time” that’s emergent. I’m calling it common time¹ as a kind of compromise because in GR there’s no sense of invariant global time while in quantum field theory (QFT) there has to be. “Local global time” was too much of an oxymoron. The idea is that “nearby” clocks become related — that we can build a foliation from spacelike slices in a small region of spacetime that somehow can be related across large regions of spacetime.

In the previous post I argued that gravity could be seen as a kind of memory effect due to soft tachyons. In an otherwise “somenified” manifold of independent times ticking at a rate ~ ℏ/m at various points in space governed by the mass m of a particle² at those points in space, we have an emergent time curvature leading to the usual weak field picture of gravity in General Relativity (GR)³. Times at different points that are completely independent and can be transformed independently by Carrollian boosts become correlated with each other over long distances — their rates all slowed by the presence of a large mass M. This is the beginning of a common time, but it’s induced by the existence of a “primary” clock in that large mass M. Two particles far from that mass but close to each other are still essentially running independent clocks in the Carrollian picture. In our current understanding of physics they should be experiencing the “common time” of flat Minkowski space. Another way: we have only created a common time where ℏ/M dominates the clock — particularly over long distances or near M. But we are in a weak field limit so by definition it shouldn’t ever dominate the clock — a contradiction and an indication we need something else. Let’s look a little closer at those tachyons.

Carrollian spacetime (see here for the background to this picture). The “clock ticks” for a system of mass m are ~ ℏ/m over a span of Carrollian time δs for a system being measured by a “minimal observer” 𝒪 consisting of a unitary operator U that would be undone by U† except for the interaction with the system of mass m. For large spacelike separation δr marked as (A) above for a given angle (i.e. minimum tachyon velocity vₛ) there is a larger span of Carrollian time δs accessible. The spread of Carrollian tachyon velocities (slopes) is δuₛ. For smaller spacelike separation marked (B), accessible δs is smaller. The region spanned by the possible tachyons is the “elsewhere” region for observer 𝒪 — orange triangles marked with (C).

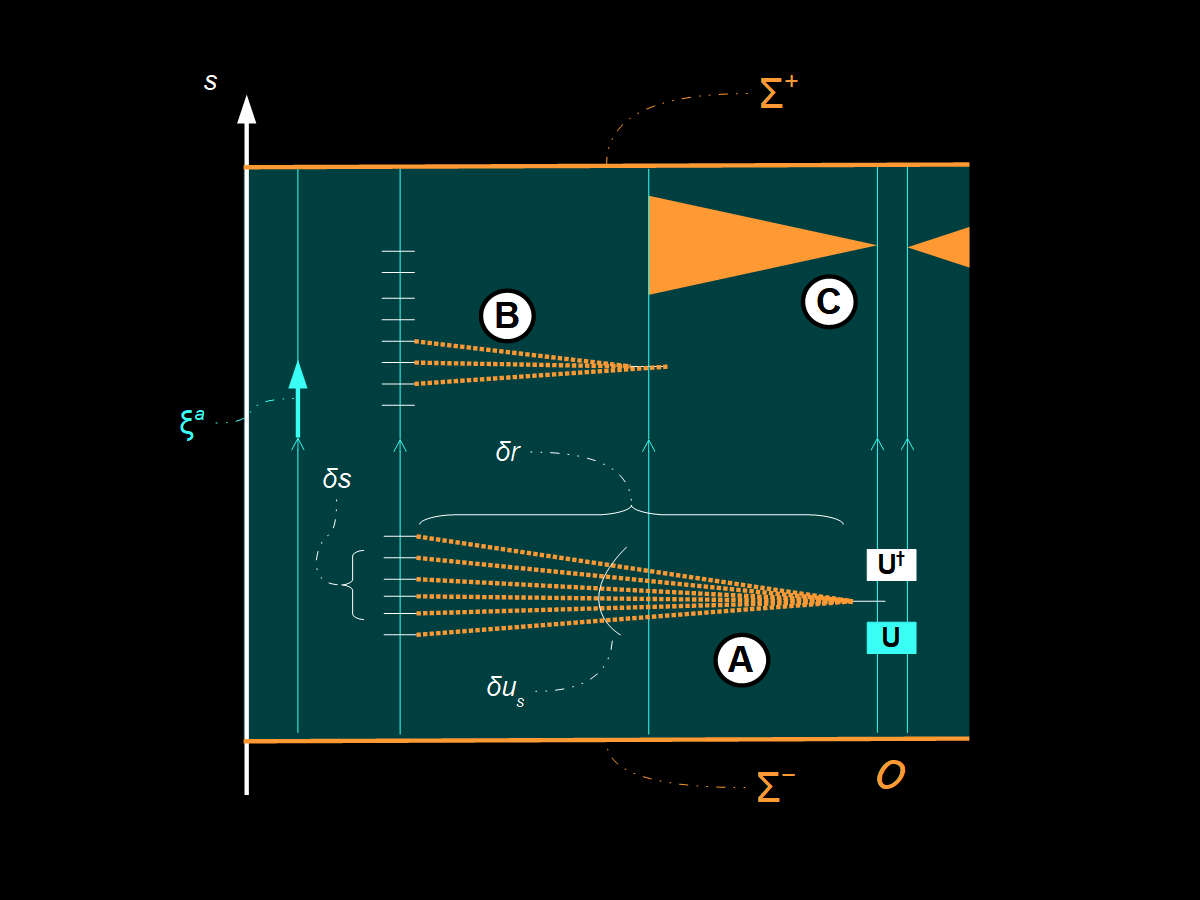
Much like how it takes infinite energy to accelerate a particle with mass to the speed of light c, in the bizarro world of tachyons it takes infinite energy to slow one down to c. On a normalized c = 1 spacetime diagram, tachyons would always move at angles less than 45°. In a sense there are two separate sectors for an observer: 1) normal particles that stay within (or on, in the case of massless particles) the observer’s future light cone δr / δt ≤ c, and 2) tachyons that are always “elsewhere” with δr / δt > c and so are not directly observable. The argument of this short series of posts (I here, II here, and III, the present one⁴) is that gravity and quantum mechanics are both the indirect effects of a “physics of elsewhere”. As I mentioned above, in II we saw how gravitational time dilation (and hence, the primary low energy effect of gravity⁵) could be introduced via the exchange of soft complex scalar (spin J = 0) tachyons⁶. In our Carrollian limit we have c ≪ vₛ where vₛ is the speed of sound for those tachyonic excitations. That < 45° condition would be δr / δs ≥ 1/vₛ for Carrollian time⁷ δs. See the graphic above.

In that graphic, we have a “minimal Carrollian observer” 𝒪 that consists of a unitary operator U along with its Hermitian conjugate U† acting on (entangling) two or more Carroll particles making up the observer. These unitary operators would cancel if not due to the tachyon perturbation interacting with a system of mass m, so a measurement consists of determining the lack of cancellation⁸ due to a kick of tachyon momentum.

The action of the system of mass m the observer 𝒪 is, um, observing is⁹

\(\displaystyle S = \int ds \, m \, u_{s} \, v_{s}\)

where uₛ ≡ dx/ds = (1/c vₛ) dx/dt = (1/c vₛ) uₜ is the “Carrollian time” velocity (it counterintuitively has units of inverse velocity). We are following references here and here that maintain the manifest Carrollian-Galilean duality except that the “large” velocity C is instead the tachyonic speed of sound vₛ. Combining an infinitesimal piece of the action with our tachyon constraint, we have

\(\displaystyle \begin{eqnarray} \frac{\delta r}{\delta s} & \geq & \frac{1}{v_{s}}\\ \delta r & \geq & \frac{\delta s}{v_{s}}\\ \delta r & \gtrsim & \frac{\hbar}{m \, \delta u_{s} v_{s}^{2}}\\ m\, \delta u_{s} \, v_{s}^{2} \, \delta r & \gtrsim & \hbar\\ \\ \delta p \, \delta r & \gtrsim & \hbar \end{eqnarray}\)

which is essentially the uncertainty principle in QM¹⁰. You might be curious about the factor of vₛ² but it is necessary to maintain units; we have:

\(\displaystyle \delta p = m \, \delta u_{s} \, v_{s}^{2} = m \frac{\delta u_{t}}{c \, v_{s}} v_{s}^{2} = m \, \delta u_{t} \, \frac{v_{s}}{c}\)

and we can take vₛ/c → 1 away from the Carrollian limit.

What’s interesting is that the momentum p is a 3-momentum¹¹ (“soft” zero energy tachyons in the Carrollian limit), space is completely “somenified”, and the time coordinates are still completely independent. No global foliation of time is necessary and the “common time” in QM is just the time coordinate for the system the observer is, um, observing. Or, another way, gravity creates a “common time” at large distance scales while quantum mechanics creates a common time at short ones¹². The Planck time tₚ = √Gℏ/c⁵, which as Carrollian time sₚ = c vₛ √Gℏ/c⁵ = ℓₚ vₛ (or, per the condition above δr / δs = ℓₚ / sₚ ~ 1/vₛ), is simply where these two pictures of common time become comparable to each other¹³. The “new physics” that arises at the Planck scale starting from classical general relativity is just quantum mechanics.

The only ingredients here are the quantum speed limit¹⁴ (QSL) and the energy condition loophole. The former are 1-dimensional quantum systems of mass m evolving on completely independent fibers. The latter gives us tachyons to play with. The Carrollian limit turns out to have just been a useful way to frame the problem — forcing you to consider tachyons as the only interesting dynamics available. Additionally, without the Carrollian limit the initial inequality is just δr / δt ≥ c which essentially says our soft tachyons are in fact tachyons. It provides no information besides the existence of tachyons.

Now I haven’t “solved quantum gravity”. I’d put this more on par with Erik Verlinde’s wisecrack. It leaves out spatial curvature for one. The measurement problem is unexplained. There’s also still a thesis-level quantity of work to do at the Planck scale where the two pictures overlap. Plus — black holes? How do they work? Another thesis. The thing I’d like to emphasize is that a consistent picture of non-relativistic quantum mechanics and Newtonian gravity was in fact inevitable because of the duality between the Galilean and Carrollian limits. It’s just that in the Carrollian limit the two theories are mixed up compared to the Galilean limit — which I think might be helpful in understanding how to treat crossing the two regimes of common time.

1. There may be a term for this in the literature, but I haven’t seen it.

2. At points not occupied by particles we would be forced to require some kind of positive energy density everywhere else in space (hmm … ) in order to prevent the time steps from becoming infinite. It’s also possible the correct interpretation is that these points don’t “really exist” and we should instead just see the VEV of the scalar tachyon field.

3. The equivalence principle in this picture showed up not because of the gravitational mass cancelling with the inertial mass in the relationship of the forces G Mm/r² = F = ma but instead via the quantum speed limit mass-energy clock ℏ/m (in Carrollian time) and the gravitational energy — so we get (G Mm/r) × (ℏ/m). There’s no longer any deep mystery in this statement since both m’s are not only mass-energy but actually the exact same mass-energy.

4. The throat clearing goes back to at least here.

5. While we look at Newton’s law of gravity as being mostly a spatial thing with F = G Mm/r², the larger effect (by factors ~c²) is actually the curvature of time — not space. It’s possible that our “spatial” picture of the gravitational force is due to a) the not-directly-observable involvement of tachyons travelling through “elsewhere” and therefore the path dependence of the historical development of science, and b) the duality between the Galilean (c → ∞) and Carrollian (c → 0) limits. You could imagine Newton’s law of gravity, the OG spooky action at a distance, being mediated by force carriers of infinite velocity. That’s essentially the message of II.

6. Scalar tachyons are the best and only kind. Q.v. representation theory of the Lorentz group [pdf].

7. As part of the duality between Carrollian and Galilean limits, we take Carrollian time to have units [s] = L²/T or action per mass.

8. It’s not really important how the observer works as the following argument doesn’t depend on U at all. This is more just setting up a framework to maybe connect to the measurement problem in quantum mechanics at some point.

9. This derives from classical single particle action in relativity using the Carrollian limit e.g. here [pdf].

10. The canonical commutation relations are considered more fundamental than the uncertainty principle, but they would be a way to enforce the condition we derived. As an aside, this is very similar to the Heisenberg microscope “derivation” of the uncertainty principle that has the same issue. The tachyons are necessary here because otherwise we would obtain the “opposite” uncertainty principle from δr / δs ≤ 1/vₛ — i.e. that δp δr ≤ ℏ. It’s interesting to think of the speed limit in special relativity is a kind of dual to the uncertainty principle. In fact, the commutation relations in quantum field theory are necessary to maintain causality [pdf].

11. See here about the invariance of the measure dp dx in terms of 3-space and 3-momentum in special relativity that is ruined by general relativity.

12. This also means “quantizing gravity” is nonsense — the necessary concept is instead consistency between two regimes of “common time”. Bold claim? Sure. GR is how you maintain common time over large distances. QM is how you maintain common time over short distances. Problem of time: sorted. (Side note: I’ve taken to using the term “quantum gravity” as simply whatever theory helps makes the two non-overlapping magisteria consistent.)

13. Per the pervious post, the Schwarzschild radius is G M/vₛ² and the Compton wavelength here would be ℏ/Mvₛ so (G M/vₛ²)(ℏ/Mvₛ) = G ℏ/vₛ³ which if vₛ/c → 1 becomes ℓₚ² i.e. the Planck length squared.

14. The traditional quantum speed limit has two forms — one in terms of the variance of the energy ΔE and one in terms of the average ⟨E⟩. It is technically the minimum of the two that is bounding, but it does mean there is an easier route to an uncertainty relation. It is unfortunately the energy-time uncertainty relation — unfortunate because it makes the argument circular as the QSL is the way physics makes rigorous sense of δE δt ≤ ℏ. Random side note: the minimum of two “velocities of information” here made me think of a possible connection.