More hand waving about quantum mechanics

It might be better characterized by arms flailing wildly like an air-driven tube man

Left: Penrose diagram with a teal right Rindler wedge for an observer A showing modular flow (Lorentz boost) from scri minus to scri plus (past and future null infinity, respectively) and a quantum “in” state Q ∈ 𝒞 exiting A’s past light cone. Right: Carrollian limit where the light cone of A closes to a line and the modular flow becomes Carrollian time s.

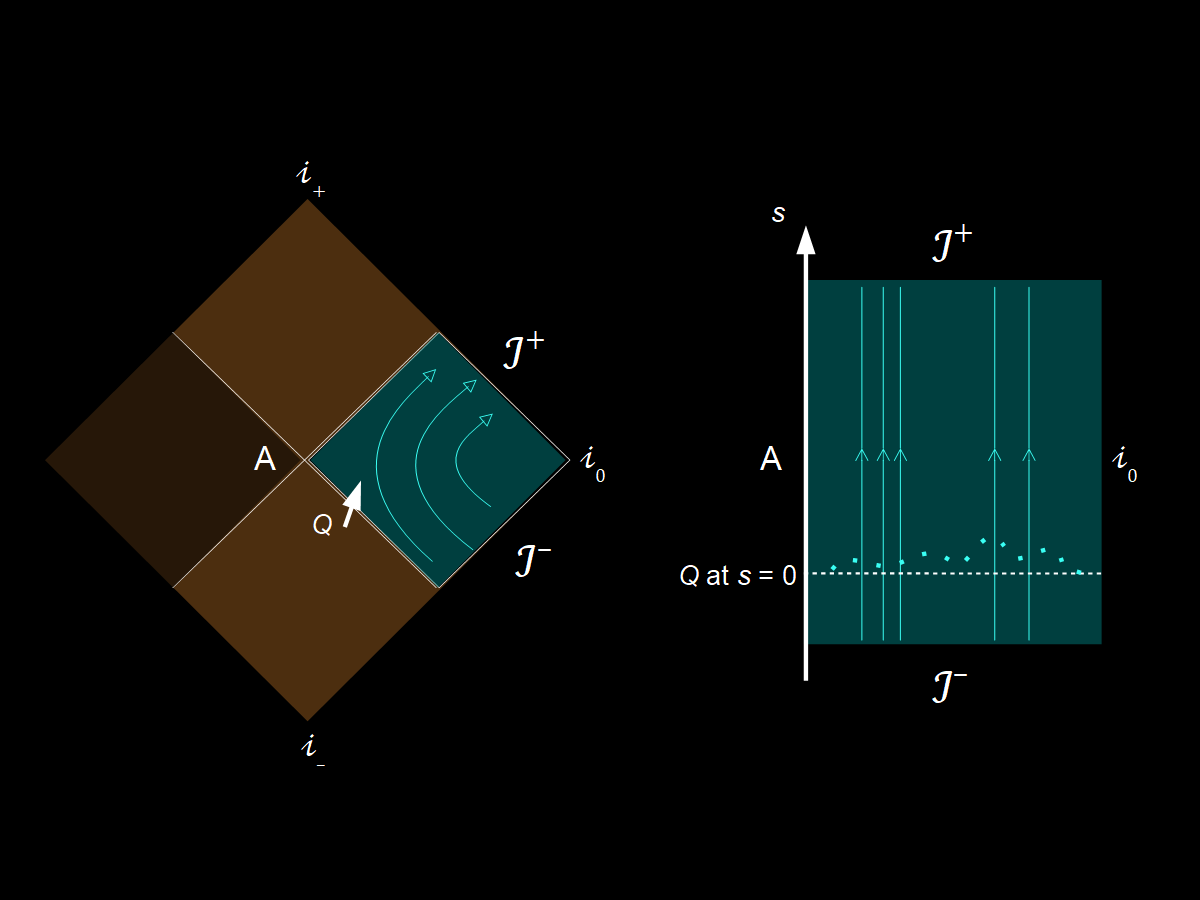
In a previous post, I worked through interpreting Barandes’ indivisible stochastic processes, ISPs, Γ(t ← 0) that consist of nothing but time t and configurations 𝒞 (notably, no sense of space!) in terms of the Carrollian limit of Minkowski space which consists of nothing but Carrollian time s and spacelike-separated points indexed by x (notably, no moving around space!). This latter picture is illustrated in the diagram at the top of this post. Like in the case of Carrollian space time, the ISP space can be viewed as a fiber bundle with flat Ehresmann connection over a base space 𝒞 ( ↔ x) with fibers parameterized by t (↔ s). I mostly say this to emphasize there’s a lot more ways these two mathematical objects are similar than just “there’s time but there isn’t anything we’d consider a path”. Also, I thought of a great word for what the Carrollian limit does to spacetime—somenification¹—and wanted a chance to introduce it. ISP space, in its Hilbert space formulation per Barandes, is also somenified.

In that post, I wrote down a dimensionless version of the Carrollian boost which is a (dimensionless) Carrollian time translation by dividing through by a constant with units of L²/T written as some length scale λ times a velocity scale v₀. Of course, L²/T is also “action per mass” and can be written as ℏ / m so that using the non-relativistic definition of momentum p = m v yields an interesting way to look at it:

\(\displaystyle \begin{eqnarray} \tilde{s} & \rightarrow & \tilde{s} ' - \frac{\textbf{v} \cdot \textbf{x}}{v_{0} \;\lambda}\\ & \rightarrow & \tilde{s} ' - \frac{\textbf{v} \cdot \textbf{x}}{\hbar / m} \\ & \rightarrow & \tilde{s} ' - \frac{\textbf{p} \cdot \textbf{x}}{\hbar} \end{eqnarray}\)

Not only are time translations measured in units of phase space, but also

\(\displaystyle \Delta p \; \Delta x \gtrsim \hbar\)

in quantum mechanics so there would be in a sense a minimum Carrollian time translation by a unit ~ ℏ. This is of course also reminiscent of “old quantum theory”, but also could give us insight to why we can only take (see Eq. 120 here but switched to dimensionful Carrollian time s)

\(\displaystyle \Gamma ^{\mathcal{D}}(s \leftarrow 0) \sim \Gamma^{\mathcal{D}} (s \leftarrow s') \; \Gamma^{\mathcal{D}} (s' \leftarrow 0)\)

after there’s been some interaction with the environment, measurement, or other “division event” 𝒟 and if s − 0 ≡ Δs > ℏ / m. or in terms of the Compton angular frequency (Zitterbewegung) ~ 1/ω (factors of c elided because this is, per the title, hand waving). The most s can be translated is 1 unit of ℏ / m so

\(\displaystyle \Gamma (\hbar/m \leftarrow 0) \neq \Gamma (\hbar/m \leftarrow \hbar/2m) \; \Gamma (\hbar/2m \leftarrow 0)\)

because there’s no such thing as Δs = ℏ / 2m.

Still: hand waving. Like in old quantum theory, I feel like I’m trapped in a phase space orbit of a minimum size around a nugget of insight. There’s still no p or x in Barandes’ ISP formulation. The closest we get is his Section V. A. (paper link) where we look at a generic operator A in the Heisenberg picture (hence the superscript H):

\(\displaystyle \frac{dA^{H}}{dt} = \frac{\partial \Theta ^{\dagger}}{\partial t} A \; \Theta +\Theta^{\dagger} A \frac{\partial \Theta}{\partial t} \)

where Θ is the time evolution operator that satisfies |Θ|² = Γ. The limit as t → 0 of the LHS of the equation above is defined as “Ȧ” and in general we have:

\(\displaystyle \left[ A, \dot{A} \right] \neq 0\)

i.e. a non-zero commutator. Per Barandes:

As a concrete example, consider a particle whose underlying position is regarded as a physical configuration, corresponding to some random variable A. If the particle’s dynamics is stochastic, in the sense that the particle can be described as a generalized stochastic system, then the particle’s velocity (or, equivalently, the particle’s momentum) will not generally have a well-defined value at all times, and will naturally be representable as an emergeable Ȧ along the lines described here.

Note that this does not say the operator A is actually position and Ȧ is actually (proportional to) momentum, only that they could be “regarded” in this way. It does not say what the commutator evaluates to, only that it could be nonzero in general. Something like the canonical commutation relation is not inconsistent withe the ISP, which is good! Note that the Hilbert space in the ISP formulation is finite (call the dimension N) so there actually cannot be a canonical commutation relation by the Stone-von Neumann theorem — only one in the limit as N → ∞.

However, you could introduce clock and shift operators (which can represent any such Hilbert space operator A if it is linear) and like in this paper (see also appendix here and references therein) generate something that looks quite a bit like position and something that looks quite a bit like momentum. It’s just a formal similarity in the limit of large N, and they’re both dimensionless, but it’s an interesting approach.

I feel like these hand waving posts always need a bullet summary of the key points because otherwise all the hand waving makes it exceedingly hard to pin down what is actually being said. It does help me to write² these things! So here we go:

• The mathematical structure³ of the ISP formulation has some similarities with the Carrollian limit.

• Somenification is fun to say.

• Since Carrollian time translations can be written in terms of phase space products, in order to be consistent with QM it would mean there is a minimum Carrollian time increment on the order of ℏ / m. That could be behind the indivisibility of the stochastic process in the ISP formulation.

• We still don’t have any position or momentum operators or canonical commutation relations in the ISP, but potentially we could construct them from clock and shift operators.

So far, I’ve really only placed the ISP and the Carrollian limit of spacetime (as a stand-in for “elsewhere”) next to each other and observed they don’t clash. But there are still serious questions:

• Where does ℏ come from?

• Where does [x, p] = 𝒾 ℏ come from? (I’m following Bousso’s conjecture in 2nd to last paragraph here, and hinted at in my previous post)

• Is the Carrollian limit even commensurate with nonrelativistic quantum mechanics or should it be commensurate with quantum field theory?

• How do we connect Carrollian boosts (time translations) to Barandes’ Θ operator?

Good enough for a Sunday afternoon post, I guess.

1. It’s not entirely unrelated to spaghettification but talking more about spacetime itself rather than matter within it. Taking the limit c → 0 turns the light cone at every point in space into a line and you can shift the time coordinate along those times fairly independently — which reminded me of a bundle of somen noodles (picture credit here):

2. There’s nowhere near enough yet for a paper. If I was a famous physicist like Maldecena Susskind, I could give a hand-wavy talk or write up one of those festschrift things but not sure who it would be in honor of.

3. The Carrollian limit inherits a lot more from its Minkowski space parent — for example the BMS group at null infinity (scri plus ℐ ⁺ and scri minus ℐ ⁻ in the picture at the top of the post). It is interesting that one of the best definitions of “particle” might well be “a representation of the BMS group”. The ISP formulation just has finite “configurations” at times s, so a deeper connection needs to be made there.