Clocking and shifting in Carrollian time

Ye olde tricke for turning a (discrete) circle into a commutator

Left: Penrose diagram with the right Rindler wedge and modular flow (aka Lorentz boosts) highlighted in teal along with a transformation (taking this as 1+1 dimensional Minkowski space) where x = −∞ is identified with x = +∞ and turned into a circle while simultaneously taking the Carrollian limit c → 0. Right: the resulting cylinder discretized as a series of dim ℌ = N lattice points with lattice separation a where ℌ is a Hilbert space.

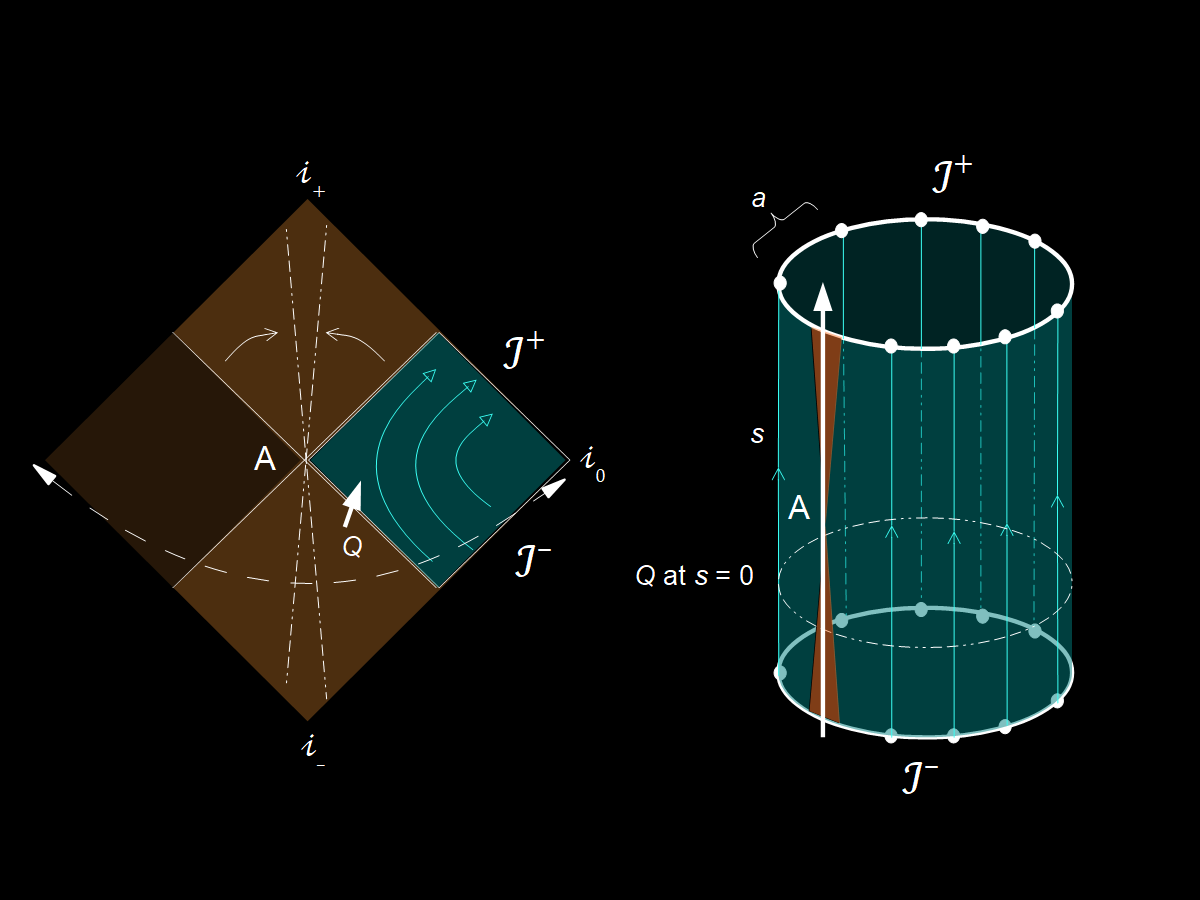
I mentioned the clock and shift operators in the previous post as a means of creating an analog of “space” X and “momentum” P from a periodic lattice of N sites where N is the dimension of the Hilbert space that can, in the limit as N → ∞, give [X, P] = 𝒾 which is (kinda, without dimensions) the canonical commutation relation. This trick¹ is basically as old as I am. My interest here is not to mechanically reproduce it, but to look at it abstractly in the lens of both the Indivisible Stochastic Process (ISP) formulation of quantum mechanics and the oddly similar Carrollian limit c → 0. We’ll drop down to 1+1 dimensions and identify “positive” spacelike infinity with “negative” spacelike infinity. In the Carrollian limit, where light cones close up to lines, these operations create a cylinder (see the diagram above). Since every spatial point on a circle is essentially a space-like separated base space for fiber parameterized by Carrollian time—somenified—there’s no real issue with discretizing the cylinder in this circular direction into N points.

Barandes showed that his (non-Markovian) ISP formulation can be construed as a finite dimensional Hilbert space (Eqns. 26-20) ℌ with dim ℌ = N. If N is prime², then any linear operator A for ℌ can be represented as linear combination of clock and shift operators B and T (for Boost and Translation) with components of the form³

\(\displaystyle T, \; B,\; T B,\; TB^{2}, \; ... T B^{N -1}\)

You can, with some effort, construct:

\(\displaystyle \begin{eqnarray} \hat{X} \; | x\rangle & = & a\; x \; | x\rangle\\ T & = & \exp \left(- i\frac{2 \pi}{ N} \frac{\hat{X}}{a} \right)\\ T\; |x\rangle & = & |x + 1\rangle \text{ for } x \neq j \end{eqnarray}\)

where x ∈ {−j … +j} with N = 2 j + 1 and “a” is the lattice spacing with (we shall declare) units of length. For x = j, this just cyclically shifts x = j to x = −j instead for prime N.

\(\displaystyle \begin{eqnarray} \hat{P} \; | p\rangle & = & k\; p \; | p\rangle\\ B & = & \exp \left( i\frac{2 \pi}{ N} \frac{\hat{P}}{k} \right)\\ B\; |p\rangle & = & |p + 1\rangle \text{ for } p \neq j \end{eqnarray}\)

Here k is the reciprocal lattice spacing with units of momentum and everything else carries over to reciprocal space (i.e. p ∈ {−j … +j} with N = 2 j + 1 and for p = j the boost shifts to p = −j for prime N). We require (and maintain)

\(\displaystyle \frac{a \; k}{\hbar} = \frac{2 \pi}{N} \)

in order to be able to take the limit N → ∞ with a → 0 and k → 0 with a k N → finite. I (suggestively) added ℏ both to make the LHS dimensionless like the RHS, and to note that a Carrollian boost (aka time shift) for dimensionless Carrollian time tilde-s is (using the position and momentum eigenvalues above):

\(\displaystyle \tilde{s} \rightarrow \tilde{s}' - \frac{(k \;p) \; (a\; x)}{\hbar} = \tilde{s}' - \frac{2 \pi \;p \; x}{N\;\hbar} \)

We could re-cast the “minimum” Carrollian time shift (mentioned here) in terms of 1/N, the dimension of the Hilbert space.

… assuming we can do this.

If we compute [X, P] we get, well, at first, a mess. In my case, it’s a mess with dimensions because a and k are dimensionful compared to other approaches. But that’s not important right now. In that limit above we find [X, P] = 𝒾 ℏ. See e.g. here [pdf], here, or here (this last one is the notation I sorta followed).

So we got a canonical commutator out of Barandes’ ISP formulation! We got a non-zero commutation relation between position and momentum in a formulation with no space. One that has an analog with no momentum because in the Carrollian limit, stuff doesn’t move⁴.

Where did we mess up? It wasn’t adding dimensionful constants as you could do the same thing with dimensionless ones. As I see it:

• Clock and shift operators induce (i.e. implicitly assume) proximity between adjacent lattice sites. This is assuming space where there is none in the ISP formalism⁵. They are an assumption in the ISP formulation.

• Clock and shift operators are inherently superluminal. A T operator instantaneously “moves” a state from one lattice site to another. They can make sense in a Galilean system (Newton-Cartan manifold), but not a Carrollian one.

Now, because of the sheer magnitude of hand-waving⁶, I need to once again write down the point:

• The “clock and shift” operator approach either assumes the answer or violates the underlying assumptions so isn’t a path to creating the canonical commutation relation. This is not the way⁷.

1. Santhanam, T. S., and Tekumalla, A. R., “Quantum Mechanics in Finite Dimensions,” Foundations of Physics 6 no. 5, (1976) 583–587. Digital, ungated copy here [pdf].

2. Having flashbacks to polynomial ring theory right now. I wouldn’t attach any significance to N needing to be prime. There are an infinite number of primes, but in this case it is almost certainly that the proof is easier for N being prime and my guess is that as N → ∞ for N not prime you could rewrite this as a set of independent modes that can be in superposition for the prime factors of N where “cross terms” become less important (i.e. fall ~ 1/N). A marvelous proof of this may or may not fit in the email limits of a substack post.

3. I’ve changed from X and Z in the reference (which are logical labels because they can be traced to the Pauli spin matrices σx and σz) to T and B for translation and boost. They are called Σ₁ and Σ₃ in the wikipedia article (where x = 1 and z = 3 in terms of indices). I should also note that this is basically related to the fact that (discrete) Fourier analysis “works” because position X and momentum P will basically become (discrete analogs) the two bases in a Fourier transforms.

4. Um. Well. Maybe?

5. There also isn’t any “space” in the “spacetime emerging from independent Hilbert spaces” approach like here, so I question if this kind of work isn’t (the original form of) question begging by assuming anything similar to clock and shift operators.

6. One benefit of handwaving is that it doesn’t actually represent information so massive quantities of it will not result in a violation of Bekenstein’s bound forming a black hole.

7. There is still the question of what I could mean by “the way”. To where? From where? I’d like to make the ISP approach more explicitly “contentful” in the sense that we’re not just relying on abstract algebra and could, e.g. write down an actual time evolution operator instead of a vague form derivable from the definition of how a time evolution operator looks.