What does the Bekenstein bound bound?

Relevant length scales and relevant degrees of freedom

The Bekenstein bound and relevant length scales

The title is a paraphrase (*cough* ripoff) of the title of a recent paper¹ trying to answer its question. In it the authors show you need limits on both encoding and decoding information in order for the Bekenstein bound to hold. The paper is of course looking at Casini’s version of the bound in a quantum field theory context², and not the original “spherical” bound which can be violated in certain dynamical situations — motivating the need for a covariant bound.

I’m not going to say anything nearly that interesting here. My mathematical abilities have a hard ceiling at dimensional analysis these days, but that’s enough to propose some dumb questions. First, two points for emphasis:

• While the “spherical” Bekenstein bound S ≤ (2π/ℏc) R E was derived using black holes, Newton’s constant G drops out implying it does not depend on gravity (general relativity). Casini’s version shows how it arises in quantum field theory (quantum mechanics + special relativity, no gravity).

• The black hole entropy/area law³ is S = (1/4) A/ℓₚ² and is not the same thing — this “bound” saturates the Bekenstein bound when the system is a black hole.

The dumb question I want to propose is:

So we say the information of a 3D black hole is encoded on its 2D surface because S ~ A/L² with [A] = L² with the Planck length as the scale as part of a holographic viewpoint, but the Bekenstein bound says S ~ R/L which has ℏc/E as the most obvious length scale⁴. Why don’t we say it’s 3D encoded in 1D?

This is even clearer with Bousso’s covariant bound

\(\displaystyle S \leq \frac{\pi \; M \; c \; \Delta x}{\hbar} = \pi \frac{\Delta x}{\lambda}\)

where λ is the Compton wavelength λₑ if M is the electron mass mₑ. Here, Δx is the smallest dimension of your system instead of being a sphere of radius R in Bekenstein’s original. It’s explicitly referencing a single dimension — a length, not an area. So where does the area come in?

Well if R E is the Schwarzschild radius (rₛ = 2 G m / c²) of your system times its rest mass-energy (E = m c²) we get:

\(\displaystyle \begin{eqnarray} 2 \pi \frac{R E}{\hbar c} & = & 2 \pi \frac{1}{\hbar c} \left( \frac{2 G m}{c^{2}} \right) m c^{2}\\ & = & \pi \frac{c^{2}}{\hbar} \left( \frac{2m}{c}\right) \left( \frac{2 G m}{c^{2}} \right) \times \left( \frac{4Gc}{4G c} \right)\\ &= & 4 \pi \left( \frac{2 G m}{c^{2}} \right)^{2} \left( \frac{c^{3}}{4 G \hbar} \right)\\ & = & 4 \pi r_{s}^{2} \left( \frac{1}{4\ell_{p}^{2}} \right)\\ & = & \frac{A}{4\ell_{p}^{2}} \end{eqnarray}\)

That factor of 1 = 4 G c / 4 G c is a bit convoluted if you ask me⁵. But there is physical content in the 2D picture — that the system’s mass falls entirely within its Schwarzschild radius (i.e. is a black hole). If that wasn’t required, you could take a more “direct” 1D route using the Schwarzschild radius purely as a scale and talk about an electron instead:

\(\displaystyle \begin{eqnarray} 2 \pi \frac{R E}{\hbar c} & = & 2 \pi \frac{1}{\hbar c} \left( \frac{2 G m_{e}}{c^{2}} \right) m_{e} c^{2}\\ & = & 2 \pi \frac{m_{e}c}{\hbar} r_{s}\\ & = & 2 \pi \frac{r_s}{\lambda_{e}} \quad (n.b.\text{wrong}) \end{eqnarray}\)

where λₑ is the Compton wavelength⁶. But the Compton wavelength is 45 orders of magnitude larger than the Schwarzschild radius of an electron, so this equation is meaningless. In fact, the Schwarzschild radius of an electron is smaller than the Planck length so is meaningless on its own. But you can kinda fix it — with a bit of general relativity. An electron has angular momentum, so the relevant scale is not the Schwarschild radius but another length scale⁷ rₐ based on J, the angular momentum = ℏ/2 for an electron, such that rₐ = J/mₑc = (ℏ/2)/mₑc = λₑ/2 and you just end up with S = π. This has the benefit of only probably being meaningless. It does hew more closely to Bousso’s bound

\(\displaystyle \frac{\pi \; m_{e} \; c \; \Delta x}{\hbar} = \frac{\pi}{2} \frac{\Delta x}{r_{a}} = \pi \frac{\Delta x}{\lambda_{e}} \)

which gives S = π if Δx = λₑ or S = π/2 if Δx = rₐ. What if we just plop in the Planck length and the Planck energy — clearly an unphysical⁸ scenario?

\(\displaystyle \begin{eqnarray} 2 \pi \frac{R E}{\hbar c} & = & 2 \pi \frac{1}{\hbar c} \sqrt{\frac{G \hbar}{c^{3}}} \sqrt{\frac{\hbar c^{5}}{G}}\\ & = & 2 \pi \frac{1}{\hbar c} \sqrt{\hbar^{2} c^{2}}\\ & = & 2 \pi \end{eqnarray}\)

Yet another combination of π and 2. But it is clear from these exercises that the “1D” approach is problematic. At least you can get results with S being o(1) which is critical for Bousso’s conjecture:

Note that for systems with small numbers of quanta (S ≈ 1), Bekenstein’s bound can be seen to require non-vanishing commutators between conjugate variables, as they prevent Mx from becoming much smaller than ℏ. One is tempted to propose that at least one of the principles of quantum mechanics implicitly used in any verification of Bekenstein’s bound will ultimately be recognized as a consequence of Bekenstein’s bound, and thus of the covariant entropy bound and of the holographic relation it establishes between information and geometry.

If we have to fall back to the area measured with a Planck scale ruler when we are considering systems at the quantum scale, then S is nowhere near o(1) that would lead to this⁹. It could mean you have to tease a macro scale quantity (macro relative to the Planck scale, but still quantum scale) out of a Planck scale change like I did here¹⁰. Or it could mean we have to make sure we are looking at accessible microstates.

Relevant degrees of freedom

One of the key pieces of the definition of entropy in terms of microstates is that those microstates need to be able to be occupied given the energy in the system — they have to be “accessible”. A straightforward example is in specific heat. At typical ambient temperatures ~ 300 K, the vibrational modes of certain molecules cannot be excited; when you use the kT/2 per degree of freedom¹¹ rule you don’t count those vibrational modes. This results in effects like the specific heat changing vs temperature:

Idealized specific heat of a diatomic gas versus temperature showing it increase from 3/2 (for the three dimensional momentum = 3 × 1/2) to 5/2 as the two additional rotational modes are excited (3+2=5) at T=T_rot, and then from 5/2 to 7/2 as the two additional vibrational modes are excited (5+2=7) at T = T_vib. Figure from wikipedia.

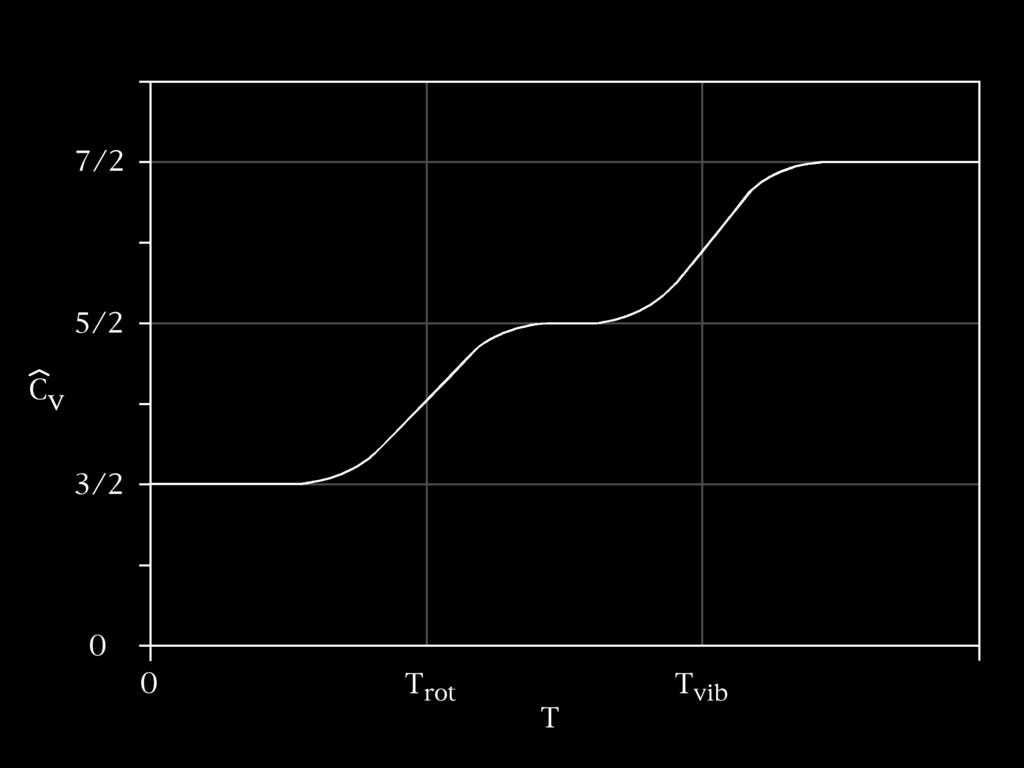
We say the higher energy degrees of freedom are “frozen out” as temperature falls and those modes no longer accessible microstates. So it could be that those Planck-scale degrees of freedom of a hypothetical quantum gravity are “frozen out” so that S ~ 1 considering accessible microstates for ordinary quantum systems. The Planck temperature is ~ 10³² K so it could make sense that the ~ 360 K for the Unruh temperature of a Rindler horizon at 1 μm from the perspective of an electron in a Hydrogen atom just doesn’t cut it.

However, we count those degrees of freedom for the entropy of a black hole when a typical black hole temperature is measured in nanokelvin! A fortiori we should count them all on the boundary of a Compton wavelength scale region (i.e. S ~ 10^46) when the Unruh temperature is ~ 360 K, right?

There is a sense that other degrees of freedom don’t “see” the Planck scale — if you have a photon of wavelength ~ Planck length it forms a black hole¹². One possible solution is that we’re really looking at changes in entropy after subtracting¹³ a background due to spacetime — that ΔS ~ 1 is the relevant quantity, not S ~ 1. In fact, Casini’s derivation of the Bekenstein bound subtracts a “background” because S is divergent ~1/L². It is not clear to me how this doesn’t just shift the problem of S being Planck scale huge to asking why isn’t ΔS also Planck scale huge (“naturalness”).

In the Carrollian limit c → 0, the length scales ℓₚ and rₛ both go to infinity (with rₛ approaching faster ~1/c²). Therefore the area of the boundary S² of a 3-ball measured in Planck areas becomes smaller.

Another possibility to “freeze out” the spacetime degrees of freedom is to take the Carrollian limit c → 0 where spacetime becomes “somenified” and, ostensibly, since there is no motion, there are fewer and fewer spacetime degrees of freedom contributing to the entropy S. In addition (or really, just another way to put it) the Planck length and Schwarzschild radius head towards infinity (the latter more quickly). Of course, the speed of light needs to get down to c ~ 10^−37 m/s (still not exactly zero) in order for ℓₚ ~ rₛ ~ λₑ.

All this just makes me want to retreat back to Bousso’s bound:

\(\displaystyle S \leq \frac{\pi \; m_{e} c \; \Delta x}{\hbar} = \pi \frac{\Delta x}{\lambda_{e}} \)

This gives a (covariant) S ~ π for an electron in free space. A bound electron to a proton would have S ~ 137 π since the Bohr radius is ~ (1/α) λₑ. In a sense, those Planck scale degrees of freedom must be “frozen out” (or it really is ΔS ~ 1 that matters). Still, the direction of the implication here is QM → S ~ 1 and not S ~ 1 → QM that a more fundamentally-based bound the Planck length could better motivate.

This has been another one of those “thinking out loud” posts that’s helpful to me to clarify what can be clarified and realize what still is vague handwaving. A short list of bullet points to close out:

• The “1D” interpretation of the Bekenstein bound is far more system-dependent (one could even say fraught) than the “2D” version. It makes sense that you’d go for the latter!

• You can’t handwave away numbers of order 10²³ (or more), so those Planck areas are going to have to be subtracted or frozen out to get S ~ 1.

1. I would like to nominate this paper’s Figure 1 as the most nonsensical figure in a physics paper for this decade. I mean what is going on? I think its supposed to be a cartoon of exciting a QFT mode on the t=0 Cauchy surface, with the causal development of the right half-plane being the right Rindler wedge — but maybe use any of those words in the caption?

2. A version that is closer to a kind of tautology due to a heavy reliance on the definition of relative entropy. Bekenstein’s original (“spherical”) bound derives from a physical argument about dropping stuff into a black hole.

3. I will be using units where Boltzmann k = 1. I may occasionally use ℏ = c = 1 (I’ll say so) when I want to write something profound like E ~ m. Throughout I will refer to the reduced Compton wavelength = ℏ/mc as “the Compton wavelength” which differs by a factor of 2π since the normal (non-reduced) version uses h instead of ℏ = h/2π. Also [X] means “units of X” which are given as lengths L, masses M, times T, etc.

4. E = ℏ ω = ℏc/λ so λ = ℏc/E with [λ] = L. Of course this is for a photon (definitely hold that thought!) but also applies for any relativistic particle where p ≫ m c.

5. It’s a couple factors of c away from (Planck force)/(Planck force).

6. Again, I use the reduced Compton wavelength throughout, but the factor of 2π would mean this formula is just the ratio of the Schwarzschild radius to the “actual” Compton wavelength.

7. Not sure it has a name? It’s the size of the ring singularity. There is also a length scale based on the charge but it is only slightly larger than a Planck length. It should be noted I am playing fast and loose with the laws of physics because this would describe a super-extremal black hole (there’s a fun paper that proposes “electron = tiny black hole”).

8. I dunno — this?

9. In the case of the Hydrogen atom, the distance to the Rindler horizon from the electron’s perspective (using the acceleration due to the Coulomb force at the Bohr radius) is on the order of 1 μm which implies S ~ 10^59. Random fun fact: the Bohmian “quantum potential” for an ℓ = 0 state (the quantum potential is proportional to the curvature of the would-be wavefunction Bohmian mechanics is trying to replicate) is equal to the Coulomb potential so serves to reduce that distance to the horizon by a factor of 2 to 0.5 μm. Also, the temperature of the Rindler horizon (Unruh temperature) is about 360 K for this acceleration.

10. Also in this post, I came up with yet another “1D” version of Bekenstein’s bound where the entropy is proportional to the Compton wavelength divided by the Planck length. Still huge! It’s about 1.5 × 10²³. Actually it’s kind of eerily close to Avogadro’s number divided by four Nₐ/4. Within 0.3%. Like 0.003. Plus there’s a 1/4 in the black hole entropy area law! It should be noted that the “α = 1/137 exactly” approximation is ten times more accurate at 0.03% error.

11. Temporarily taking Boltzmann k ≠ 1.

12. This is a way you can “derive” the Planck length.

13. Or straight up ignoring it as a “thermal bath”.